Resolviendo un sudoku difícil.

El siguiente sudoku fue publicado en La Tercera del Domingo pasado. Está catalogado como difícil.

Se puede resolver 6 casillas de inmediato, y el sudoku queda:



Anotando las candidatos posibles para cada celda aún vacante, el sudoku se ve así:

En la tercera caja, el candidato "1" está sólo en la primera fila, por Pointing Pair se pueden borrar los "1" que existen en las celdas rosadas. Igual cosa sucede con los "9" en la tercera caja; por lo mismo se pueden borrar los "9" de las casillas rosadas. Por otro lado, también por Pointing Pair se puede eliminar el candidato "2" de la celda azul (notar que en la primera caja, sólo la tercera fila tiene "2"). Luego el sudoku queda como sigue:

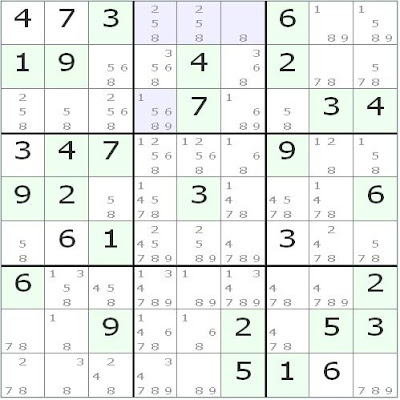
Se puede ver que el "8" de la primera fila puede resolverse de inmediato. El sudoku queda:

El par gemelo amarillo de la primera fila nos permite borrar el "5" de la casilla azul de la primera fila. De igual modo, el par gemelo amarillo de la tercera fila nos permite borrar los candidatos "5" y "8" de las casillas azules de la tercera fila, así como los mismos candidatos de la casilla roja de la misma fila, quedando sólo posible en dicha casilla el candidato "2". En consecuencia se nos forma un nuevo par gemelo (7 y 8) en las casillas amarillas de la primera columna, lo cual nos permite eliminar el candidato "8" de la celda roja de la primera columna y cuarta caja, quedando posible sólo el candidato "5" en dicha celda. Además pueden borrarse los candidatos "8" de la caja siete (debido al par gemelo amarillo 7-8 existente en dicha caja), con lo cual ya sabemos dónde están en esta caja el 3, el 1, el 5, el 4 y el 2. A partir de aquí, siempre queda posible un único candidato para al menos alguna celda aún por resolver del sudoku, con lo cual ya es fácil resolverlo sin aplicar ninguna técnica avanzada. La solución final es: